Center for Molecular Spectroscopy and Dynamics

4-A. Motivation

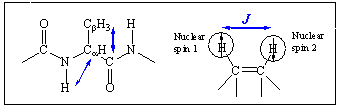
The very first step toward understanding chemical and biological properties of a given protein is to determine its three-dimensional structure. Two of the most widely used methods are X-ray crystallography and 2D NMR (nuclear magnetic resonance) spectroscopy. As mentioned in Sec.1, the X-ray crystallography requires a sample in a crystalline form. Although we have seen a growing interest of time-resolved X-ray diffraction measurement, still the sample should be a molecular crystal so that this technique is not suitable for the time-resolved investigation of the structural change of proteins in solution. Secondly, the 2D NMR, though it can be used to determine 3D protein structure in solution, cannot be used to study relatively fast dynamics and conformational fluctuation and transition due to its intrinsically limited time resolution. Thus, an alternative third experimental method that is capable of both time- and frequency-resolution has been sought. In this regard, the coherent multidimensional spectroscopy has been considered to be a potentially useful method, which might overcome both difficulties associated with X-ray crystallography and 2D NMR spectroscopy. The principle idea proposed at the beginning of the CMDS was born while the P.I. tried to make a direct comparison of various nonlinear vibrational spectroscopy with 2D and 3D NMR spectroscopies. The one-dimensional NMR spectroscopy is to measure the free induction decay of the nuclear spin system after a single radio-wave pulse passing through the sample. The time-resolved free induction decay signal can be Fourier-transformed to obtain 1D NMR spectrum. The spectral analysis of a 1D NMR spectrum provides direct information on the existence of nuclear spins and chemical shifts revealing their distinctively different chemical environment so that it can be used to extract information on the molecular structure of an unknown sample. Although the conventional 1D NMR spectroscopy has been found to be extremely useful in identifying unknown chemicals, the 1D NMR spectra of proteins and nucleic acids were found to be very complicated due to overlapping spectral bands, which prohibit further analysis for protein structure determination. In order to overcome this so-called spectral congestion problem, several 2D NMR techniques were developed and they involve two or more radio wave pulses to probe the 2D spin coherence state created by the nonlinear field-matter interactions. Detailed measurement of the spin-spin coupling constants J, can then provide far more direct information on the 3D protein structure (2D-COSY NMR). As can be seen in the above pictorial scheme, the spin-spin coupling constant J depends on the relative distance and orientation of the two nuclear spins, meaning that the J value is a function of the precise 3D conformation of the molecule of interest. An alternative way to study the spin-spin interaction is to measure the nuclear Overhauser enhancement effect that reflects the coherence transfer between any two quantum spin states. This 2D nuclear Overhauser enhancement NMR spectroscopy (2D-NOESY NMR) was shown to provide information on the relative distance between two spins so that the 2D-NOESY spectrum can be considered as a map of inter-nuclear distance. Particularly, the existence of a cross peak means that the two protons (for example, proton NMR) are located within 5 Å distance.

Similar to the 1D NMR, the linear vibrational spectroscopies, such as infrared absorption and Raman scattering spectroscopies, involve one infrared or visible fields and the spectra are plotted as a function of a single tunable frequency, so that these methods are essentially one-dimensional spectroscopies. Other than the radiation frequency used in the absorption spectroscopy, both 1D NMR and 1D IR absorption spectroscopies are identical in the sense that an absorption cross section is measured. Noting that the 2D or 3D NMR spectroscopy was developed by using multiple radio-wave pulses to create multidimensional nonlinear polarization, one can use multiple IR or visible pulses to create multidimensional coherence states that in turn produces a spontaneous emission field being detected. In order to clarify this natural extension of 1D vibrational spectroscopy to 2D or 3D vibrational spectroscopy, consider the following figure, which is similar to the one shown above for schematic description of 2D NMR spectroscopy.

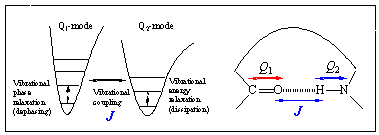
A typical IR absorption spectroscopy provides information on the transition probabilities of each individual vibrational modes, Q_j. This one-quantum transition has been called a fundamental transition. Any pair of vibrational degrees of freedom, however, are coupled to each other via mechanical anharmonicity associated with anharmonic potential terms as well as via electric anharmonicity originating from nonlinear coordinate dependencies of electronic dipole and polarizability. In general, these coupling-induced transition probabilities are extremely small in comparison to the fundamental transition probabilities so that it is difficult and sometime impossible to identify these transitions from an infrared absorption spectrum. Noting that the vibrational coupling constants J are highly sensitive to the 3D molecular structure in either gas or condensed phases, one would like to quantitatively measure these vibrational coupling constants revealing critical information on the 3D conformation of the polyatomic molecule. Due to the limitation of those 1D vibrational spectroscopies in quantitatively measuring these small quantities (J values, for example), a natural step toward an achievement of this goal is to use coherent multidimensional vibrational spectroscopy utilizing multiple IR or visible pulses.

4-B. Hypothesis

Based on the logical reasoning stated above, we proposed two hypotheses. (1) There is a one-to-one correspondence between the 3D structure of protein and its multidimensional spectrum. (2) Once the multidimensional spectrum is time-resolved by using ultrafast laser pulses, the structural change of chemical species involved either in chemical reaction or in physical process can be resolved in time-domain.

4-C. Qualitative Pictures

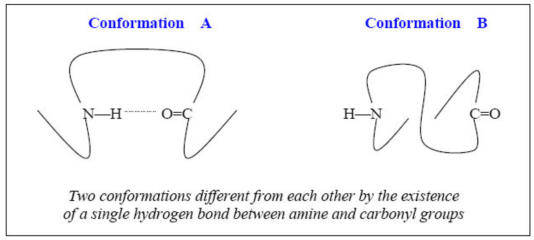
Noting that the secondary and tertiary structures of proteins are stabilized via various intra- and intermolecular interactions such as hydrogen-bond, electrostatic interaction, van der Waals interaction, hydrophobic interaction etc., one can extract vital information on the 3D polypeptide structure from vibrational couplings specifically depending on these interactions. For instance, the carbonyl oxygen and hydrogen atom in N-H group can form a single hydrogen bond, which is found in a- helix or pleated b-sheet polypeptides. Suppose that the structure of a given protein is likely to be one of the two conformations shown in the following figure below. A critical difference between the A- and B-conformations is the very presence of a specific hydrogen bond. If there is a hydrogen bond between amine and carbonyl groups as can be seen in the A-conformation, the amide I mode, which is the C=O stretching mode (with frequency of w_I), can be strongly coupled to the amide III mode (with frequency of w_III), which is the N-H bending mode. Therefore, the cross-peak intensity in the case of conformation A is likely to be larger than that of the conformation B. In reverse, if there is a relatively strong cross-peak at (w_I and w_III) in a given 2D vibrational spectrum, one can assume that the correct structure is A rather than B. Of course, there are other localized amide I and III modes in a polypeptide so that the 2D vibrational spectrum would again be spectrally congested so that one might not be able to selectively measure this cross peak. However, introducing isotopes such as ¹³C, ¹⁸O, and D (deuterium) for the two target modes and using doubly vibrationally resonant enhancement effect of the IR-IR-vis four-wave-mixing spectroscopy, it will be experimentally feasible to measure the absolute intensity of this cross peak.

This is just a qualitative picture, though a highly simplified scheme, demonstrating how a variety of coherent multidimensional vibrational spectroscopies can be of use to determine 3D polypeptide structure in condensed phases. As will be discussed later in Sec.5, the angle between any two transition dipoles can be measured from the ratio of cross-peak intensity to diagonal-peak intensity in a given 2D IR pump-probe or photon echo spectrum. Furthermore, the conventional vibrational circular dichroism (VCD) spectroscopy can provide quantitative information on the angle between vibrational transition electric and magnetic dipoles. Then, the 2D-VCD spectroscopy that was theoretically proposed by the CMDS recently (J. Chem. Phys. in press (2003)) can be used to estimate the angle between the transition dipole of one vibrational mode (such as local amide I mode of the jth peptide) and the transition magnetic dipole of the other vibrational mode (that of the kth peptide). The set of angles thus measured will serve as a set of conformational constraints drastically reducing the total number of allowed 3D structures of the target polypeptide